Site map :
Last upgrade to the site:
august 10th, 2002.
There has been
access to my Lego pages since creation.
This is an unofficial LEGO® web site.
LEGO® is a trademark of the LEGO® Group of companies
which does not sponsor, authorize or endorse this site.
You can visit the official LEGO website at: http://www.lego.com
Copyright 1996, 2000, Denis Cousineau
| |
Part 1: How to measure the strength of a motor
We all did a robots in the past. We envisioned a
sparkling R2D2, or a powerful arm, but invariably, we have been deceived by it’s
speed: it is slow.
Making a robot with Lego motors implies a kind of
trade-off: Either we have a fast-motion robot, but the smallest obstacle stops
it, or we have a vigorous robot, but speed is reduced to a few inch a minute!
Solution consist in using two or more motors in
combinations. However, we must make sure the solution is worth the trouble. I
once built a six-legged ant. With only one motor, the speed was very slow. I
therefore added another motor at the other extremity. Speed didn’t changed
at all because the increase in total weight counterbalanced the effect of the
second motor!
In the following, we show how to calculate the speed
of rotation of a motor. We then show how to calculate the torque, that is, the
strength of the motor turning at a given speed. Finally, the results for Lego
motors are shown. The next link will give hints on how to connect two motors
in parallel.
 | Measuring speed of rotation of a motor
In order to measure the speed of rotation, we have
to reduce it by a known proportion first. To do this, we need gears.
Using one 24-tooth gear and one 8-tooth gear
connected together, we obtain a reduction (or an increase) by a factor of
3:1. If we want a reduction in speed, place the smallest gear (the 8-tooth)
right on the source of rotation. This is a first step in the right
direction. However, the speed of the Lego motors is so high that one such
reduction is not enough. We need to reduce speed another time.
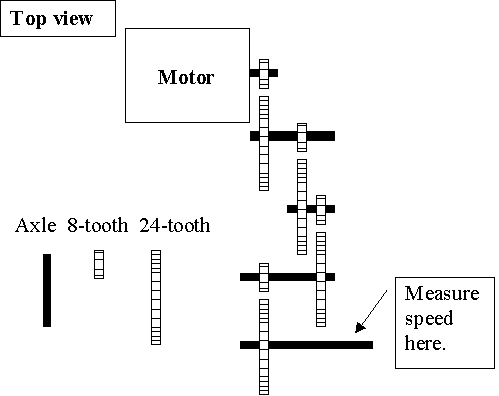
Using 4 combination of 24:8 gears, I have been
able to reduce enough the speed of the motor. Overall, the reduction is of 4
times 3:1. Thus, I reduced the motor by a factor of 3 X 3 X 3 X 3, that is,
81 times. Now, it can be measured with a watch. |
For example, if we count 15 rotations in a period of
15 seconds, we have 60 rotations per minutes (60 RPM). Since, speed was
reduced 81 times, the speed of the motor must be 60 X 81, that is 4860 RPM.
Data obtained from my own Lego motors are given in the last section.
| Measuring torque. |
Torque is the name given to the strength of rotating
device. The exact formula is given by:
tau = r F sin q
where q is the angle between the weight to move and
the lever arm. The next figure illustrate this.
Since in most application (as in our drawing), the
angle q is 90 degrees, sin q
equals one, and thus, we can ignore this factor. r is the length of the lever
arm, and F is the force exerted by the lever arm. The torque of the motor is
found when equilibrium is attained, that is, the mass M remains suspended in
the air.
Torque is a constant for a given motor. In order to
lift twice as much, we need to reduce the lever arm by half. Conversely, if
lever arm is double, half the weight can be lifted. It is seen from the
equation tau = r F. F represents the mass supported by a lever arm of 1
unit in length. However, using gears to reduce speed changes the torque,
so I will always perform my measures with a specific speed reduction.
For example, you want to measure the torque of a motor.
After many trials, you notice that it is at equilibrium when a weight of 5
kilograms is placed at the extremity of a lever arm 20 cm long. Therefore, the
motor is having a torque of 5 Kg X g X 0.20 m = 1 N m. g is the gravitational
constant (about 10 m / s / s). The unit N (Newton) measures the force in
linear physics, and N m (Newton per meter), force for rotating device. The
"per meter" represents the fact that the torque of a motor depends
on the length of the lever arm.
In physics, a weight is determined both by the mass of
the object and the gravitational field in which it is placed. Since it is
unlikely that you will build a lunar robot using Lego, I will ignore the
gravitational constant g, and assume that M is the number of bricks
(standard 2 X 4 bump bricks) lifted. Further, I will measure the length of the
lever arm in term of bump. Therefore, a very powerful motor might have a
torque of 1000 bricks X 16 bumps, or 16000 bricks X bumps. It means it can
lift (or be at equilibrium with) 1000 standard bricks attached to a 16-bump
long lever arm. It also means that if I reduce the length of the lever arm to
8 bumps, it will lift 2000 bricks. With a length of 64 bumps however, only 250
bricks will be lifted. However, it is important to mention if the motors has
been slowed down or not using various combinations of gears.
In order to be precise, I should include in my
calculation the weight of the thread used, and also the weight of the lever
arm, but in the following, I will assume it negligible.
| Results obtained with Lego motors
In order to make my measures, I build up a
tower. At the top, I put the motor (or motors) with the gears to reduce the
speed, and attached a block of blocks to it.
 | Standard motor
 In
all my test with standard 9v Lego motors, I reduced the speed 81 times
(that is, 4 combinations of 24:8 gears). I also used a lever arm 8-bump
long.
Speed: I measured 10 rotations in a 15-second
laps. It means the motor is turning at 3200 RPM (revolution per
minutes). Try yourself: 10 turns in 15 seconds means 40 RPM. Therefore,
before the 81 times reduction, the speed is 40 X 81, or 3240 RPM to be
more precise.
Torque: One motor nearly lifted 110 bricks. The
torque is thus 110 bricks X 8 bumps, or 880 bricks X bumps.
|
| New 9v motors
 The
new 9v motors provides a compact motors with reduced speed. As you will
see, not only the speed is reduced, but torque is also greatly enhanced.
I reduced the speed using two 40:5 gear
combinations. I measured slightly less than 15 turns in one minute. This
mean an overall speed of 15 RPM X 5:1 X 5:1, or about 370 RPM. It
could lift a weight of 240 bricks. the torque is therefore 240 bricks X
8 bumps, or 1920 bricks X bumps. This is clearly more than twice that of
regular 9v motors. No doubt, these motors are to be preferred in all
case. Unless you need high speed, in which case, adding extra gears to
increase the speed of the new motors might alleviate the gains. |
| Micro-motor
 Since
micro-motors have a very slow speed, I didn’t reduced the speed.
Speed: It turns at a speed of 9 rotations in a
period of 15 seconds. Speed is therefore 36 RPM.
Torque: One micro-motor barely lifted 8 bricks
with a lever arm of 8 bump. Its torque, 8 bricks X 8 bumps, or 64 bricks
X bumps, is 14 times less than standard motors. Clearly, these
micro-motors are of very limited use in you robots. Yet, Richard Caudle
did complete a robot using only two micro-motors. This is maybe the
lightest robot ever seen on the internet! See more at Baby
Scratchy robot. |
|
|
The results are summarized in the table below:
| Motor |
Normal speed (RPM) |
Torque (Lego units) |
Torque (metric units) |
at a speed of |
 |
3240 |
880 bricks X bump
|
1.760 Kg X cm |
40 RPM |
 |
370 |
1920 bricks X bump |
3.840 Kg X cm |
15 RPM |
|
36 |
64 bricks X bump |
0.128 Kg X cm |
36 RPM |
|
|
